Angles Formed By Intersecting Lines
We are going to study related angles such as side by side angles, linear pair of angles and vertically contrary angles.
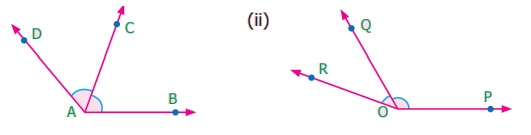
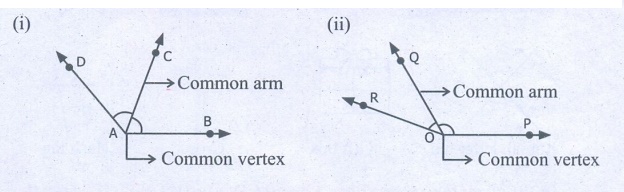
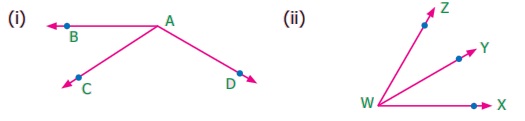
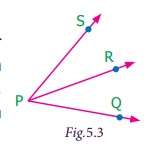
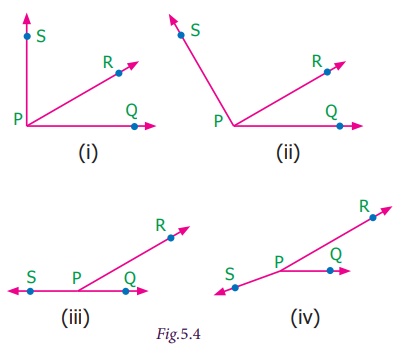
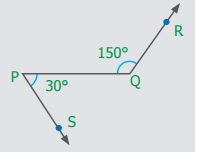
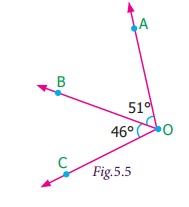
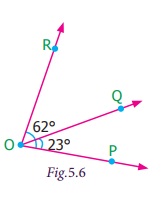
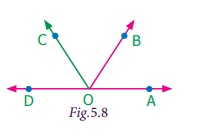
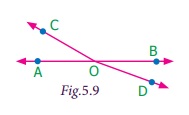
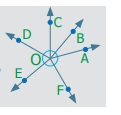
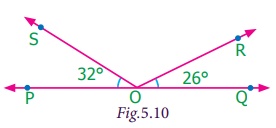
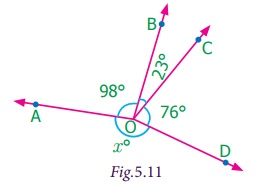
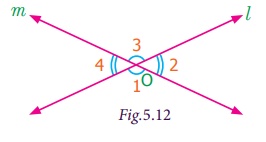
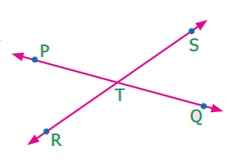
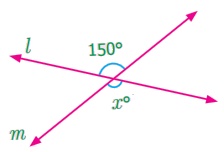
Pair of Angles formed by Intersecting Lines We are going to study related angles such as adjacent angles, linear pair of angles and vertically opposite angles. one. Adjacent angles The teacher shows a film of sliced orange with angles marked on it. Read the conversation between the teacher and students. Instructor : How many angles are marked on the picture? Can you proper name them? Kavin : Three angles are marked on the movie. They are ∠ AOC, ∠ AOB and ∠ BOC Teacher : Which are the angles seen side by side to each other? Thoorigai : Angles such as ∠ AOB and ∠ BOC are side by side to each other. Teacher : How many vertices are at that place? Mugil : In that location is merely one common vertex. Teacher : How many arms are at that place? Name them. Amudhan : In that location are iii arms. They are Teacher : Is at that place any common arm for ∠ AOB and ∠ BOC? Oviya : Yes. Teacher : What can you say almost the arms Kavin : They lie on the either side of the common arm Teacher : Are the interiors of ∠ AOB and ∠ BOC overlapping? Mugil : No. Their interiors are non overlapping. Instructor : Hence the two angles, ∠ AOB and ∠ BOC have one mutual vertex (O), one common arm ( Such pair of angles ∠ AOB and ∠ BOC are called next angles. So, 2 angles which have a common vertex and a common arm, whose interiors do not overlap are called adjacent angles . Now observe the Fig.v.2 in which angles are named ∠ 1, ∠ 2 and ∠ three. Information technology can exist observed that there are two pairs of adjacent angles such equally ∠ ane, ∠ 2 and ∠ ii, ∠ iii. So what nigh the pair of angles ∠ one and ∠ 3? They are not adjacent because this pair of angles have a mutual vertex merely they do non accept a mutual arm as ∠ two is in betwixt ∠ 1 and ∠ iii. Besides interiors of ∠ one and ∠ 3 practice non overlap. Since the pair of angles does not satisfy one amidst the iii conditions they are non adjacent. Think In each of the following figures, observe the pair of angles that are marked as ∠ 1 and ∠ 2. Do you lot recall that they are side by side pairs? Justify your respond. Endeavour these 1. Few real life examples depicting side by side angles are shown below. Can y'all requite iii more than examples of adjecent angles seen in real life? two. Discover the six angles marked in the moving-picture show shown. Write any four pairs of next angles and that are not. adjacent angles ∠ A and ∠ B, ∠ B and ∠ C ∠ C and ∠ D, ∠ D and ∠ Due east ∠ E and ∠ F Not adjacent angles ∠ Aand ∠ C ∠ B and ∠ D ∠ C and ∠ East ∠ Dand ∠ F ∠ Aand ∠ D 3. Place the mutual arm, common vertex of the side by side angles and shade the interior with two colours in each of the post-obit figures. 4. Name the adjacent angles in each of the following figure. (i) ∠ BAC and ∠ CAD (ii) ∠ ZWY and ∠ YWX 2. Linear pair Detect the Fig.5.iii ∠ QPR and ∠ RPS are adjacent angles. It is articulate that ∠ QPR and ∠ RPS together volition make ∠ QPS which is acute. When ∠ QPR and ∠ RPS are increased ∠ QPS becomes (i) right angle, (two) birdbrained angle, (iii) straight angle and (4) reflex angle as shown in Fig.5.4. If the resultant angle is a direct angle then the angles are called supplementary angles. The side by side angles that are supplementary lead us to a pair of angles that lie on directly line (Fig.5.4(iii)). This pair of angles are called linear pair of angles. Try these ane. Observe the post-obit pictures and find the other angle of linear pair. The other angle (i) 96° (ii) 94° (three) 21o Think Observe the figure. In that location are two angles namely ∠ PQR = 150° and ∠ QPS = 30°. Is all this pair of supplementary angles a linear pair? Discuss. Case 5.1 In Fig. 5.5, discover ∠ AOC . Solution ∠ AOC = ∠ AOB + ∠ BOC = 46° + 51° = 97° Case five.two If ∠ POQ = 23° and ∠ POR = 62° then find ∠ QOR Solution We know that ∠ POR = ∠ POQ + ∠ QOR 62° = 23° + ∠ QOR Subtracting 23° on both sides 62° – 23° = 23° + ∠ QOR – 23° ∠ QOR = 39° Instance v.iii Which of the following pair of adjacent angles volition make a linear pair? (i) 89°, 91° (ii) 105°, 65° (three) 117°, 62° (four) 40°, 140° Solution (i) Since 89° + 91° = 180°, this pair will be a linear pair. (ii) Since 105° + 65° = 170° ≠ 180°, this pair cannot brand a linear pair. (iii) Since 117° + 62° = 179° ≠ 180°, this pair cannot make a linear pair. (iv) Since 40° + 140° = 180°, this pair will exist a linear pair. Instance five.iv Find the missing angle. Solution (i) Since the angles are linear pair, ∠ ACD + ∠ BCD = 180° 123° + ∠ BCD = 180° Subtracting 123° on both sides 123° + ∠ BCD – 123° = 180° – 123° ∠ BCD = 57° (ii) Since the angles are linear pair, ∠ LNO + ∠ MNO = 180° 46° + ∠ MNO = 180° Subtracting 46° on both sides 46° + ∠ MNO – 46° = 180° – 46° ∠ MNO = 134° Example v.5 Two angles are in the ratio 3:2. If they are linear pair, find them. Solution Permit the angles be threex and 2x Since they are linear pair of angles, their sum is 180°. Therefore, 3x+2x = 180° 5x = 180° x = 180º / 5 10 = 36° The angles are 310 = 3×36 = 108° ii10 = 2×36 = 72° More on linear pairs Amudhan asked his instructor what would happen if he drew a ray in between a linear pair of angles? The teacher told him to draw it. Amudhan drew the ray as shown in Fig.5.8. Teacher asked Amudhan, "what can you say about the angles ∠ AOB and ∠ BOC?". He said that they are side by side angles. Also information technology is true that ∠ AOB + ∠ BOC = ∠ AOC. The teacher besides asked about the pair of angles ∠ AOC and ∠ COD . He replied that they are linear pair. Therefore, their sum is 180° i.e. ∠ AOC + ∠ COD = 180°. Combining these two results we become ∠ AOB + ∠ BOC + ∠ COD = 180°. Thus, the sum of all the angles formed at a point on a straight line is 180°. Think What would happen to the angles if nosotros add 3 or 4 or 5 rays on a line as given below? We can learn i more result on linear pairs. Observe the post-obit Fig.5.ix. AB is a directly line. OC is a ray meeting AB at O . Here, ∠ AOC and ∠ BOC are linear pair. Hence ∠ AOC + ∠ BOC = 180° Besides, OD is another ray coming together AB at O . Again ∠ AOD and ∠ BOD are linear pair. Hence ∠ AOD + ∠ BOD = 180° Now, ∠ AOC , ∠ BOC , ∠ AOD and ∠ BOD are the angles that are formed at the point O . We tin can observe that ( ∠ AOC + ∠ BOC ) + ( ∠ AOD + ∠ BOD ) = 180° + 180° = 360°. So, the sum of the angles at a signal is 360°. Think Tin y'all justify the post-obit statement. ∠ AOB + ∠ BOC + ∠ COD + ∠ DOE + ∠ EOF + ∠ FOA = 360°? Example 5.6 From Fig.5.10, detect the measure of ∠ ROS . Solution We know that ∠ QOR + ∠ ROS + ∠ SOP = 180° 26° + ∠ ROS + 32° = 180° ∠ ROS + 58° = 180° Subtracting 58° on both sides Nosotros go, ∠ ROS = 180° – 58° = 122° Example 5.7 In Fig. 5.11, notice the value of x ° Solution 98° + 23° + 76° + 10° = 360° 197° + x° = 360° x ° = 360° − 197° = 163° 3. Vertically opposite angles Nosotros have already studied almost intersecting lines. Observe the Fig.v.12. At that place are two lines namely l and g which are intersecting at a indicate O and forming 4 angles at that betoken of intersection. They are ∠ 1, ∠ ii, ∠ 3 and ∠ iv. Consider any one angle among this say ∠ 1. The angles which are side by side to ∠ 1 are ∠ 2 and ∠ 4, ∠ 3 is a non-next bending. Similarly, for the remaining three angles two angles will exist adjacent and one bending will be non-adjacent. Nosotros can discover that an angle and its non-adjacent angle are simply opposite to each other at the point of intersection O (vertex). Such angles which are opposite to each other with reference to the vertex are called vertically opposite angles. When two lines intersect each other, 2 pairs of not-side by side angles formed are called vertically opposite angles. Try these one. Four existent life examples for vertically reverse angles are given below. Give four more examples for vertically contrary angles in your surrounding. 2. In the given effigy, two lines iii. Name the two pairs of vertically opposite angles. ∠ PTS and ∠ RTQ ∠ PTR and ∠ STQ 4. Notice the value of x° in the figure given below. 10 o = 150o Activity On a paper draw ii intersecting lines 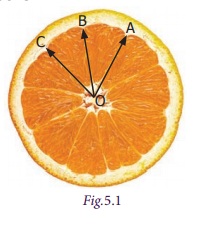
![]() , OB and
, OB and ![]()
![]() is the common arm for ∠ AOB and ∠ BOC .
is the common arm for ∠ AOB and ∠ BOC . ![]() and
and![]() ?
? ![]() .
. ![]() ), other two arms (
), other two arms ( ![]() and
and ![]() ) prevarication on either side of the common arm and their interiors do not overlap.
) prevarication on either side of the common arm and their interiors do not overlap. 







![]() and
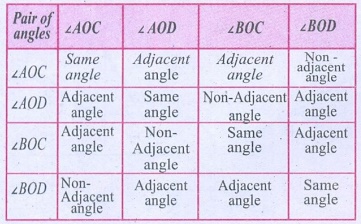
and![]() intersect at O. Notice the pair of angles and complete the following table. One is done for you.
intersect at O. Notice the pair of angles and complete the following table. One is done for you.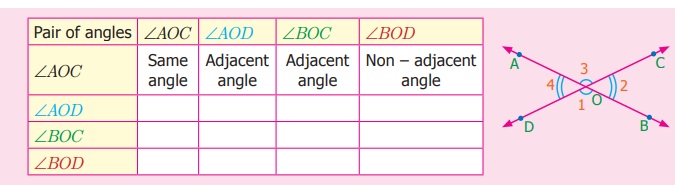
![]() and
and ![]() . Let the two lines intersect at O . Label the two pairs of vertically opposite angles as ∠ ane, ∠ 2 and ∠ 3, ∠ 4. Make a trace of angles ∠ 2 and ∠ 3. Place the traced bending ∠ 2 on angle ∠ 1. Are they equal? Place the traced angle ∠ iii on angle ∠ 4. Are they equal? Continue the same for 5 different pair of intersecting lines. Record your observations and discuss.
. Let the two lines intersect at O . Label the two pairs of vertically opposite angles as ∠ ane, ∠ 2 and ∠ 3, ∠ 4. Make a trace of angles ∠ 2 and ∠ 3. Place the traced bending ∠ 2 on angle ∠ 1. Are they equal? Place the traced angle ∠ iii on angle ∠ 4. Are they equal? Continue the same for 5 different pair of intersecting lines. Record your observations and discuss.
Tags : Geometry | Term 1 Affiliate 5 | seventh Maths , 7th Maths : Term 1 Unit 5 : Geometry
Report Fabric, Lecturing Notes, Assignment, Reference, Wiki description explanation, cursory detail
7th Maths : Term 1 Unit five : Geometry : Pair of Angles formed past Intersecting Lines | Geometry | Term i Affiliate 5 | 7th Maths
Angles Formed By Intersecting Lines,
Source: https://www.brainkart.com/article/Pair-of-Angles-formed-by-Intersecting-Lines_44170/
Posted by: walkerdeboyfaing.blogspot.com


0 Response to "Angles Formed By Intersecting Lines"
Post a Comment