Tangent Lines Of A Circle
Unit Circle
A unit circle from the proper noun itself defines a circle of unit radius. A circumvolve is a closed geometric figure without whatsoever sides or angles. The unit circle has all the backdrop of a circumvolve, and its equation is besides derived from the equation of a circle. Farther, a unit of measurement circle is useful to derive the standard angle values of all the trigonometric ratios.
Here we shall learn the equation of the unit circle, and understand how to represent each of the points on the circumference of the unit of measurement circle, with the help of trigonometric ratios of cosθ and sinθ.
| i. | What is a Unit Circle? |
| 2. | Finding Trigonometric Functions Using a Unit Circle |
| 3. | Unit of measurement Circumvolve with Sine Cos and Tan |
| iv. | Unit Circumvolve Chart |
| v. | Unit of measurement Circle and Trigonometric Identities |
| 6. | Unit of measurement Circle Pythagorean Identities |
| vii. | Unit of measurement Circle and Trigonometric Values |
| 8. | Unit Circle in Circuitous Plane |
| ix. | FAQs on Unit of measurement Circle |
What is Unit of measurement Circle?
A unit circumvolve is a circle with a radius measuring ane unit. The unit circle is generally represented in the cartesian coordinate plane. The unit of measurement circle is algebraically represented using the second-degree equation with ii variables 10 and y. The unit circle has applications in trigonometry and is helpful to find the values of the trigonometric ratios sine, cosine, tangent.
Unit of measurement Circle Definition
The locus of a signal which is at a distance of one unit of measurement from a fixed point is called a unit circle.
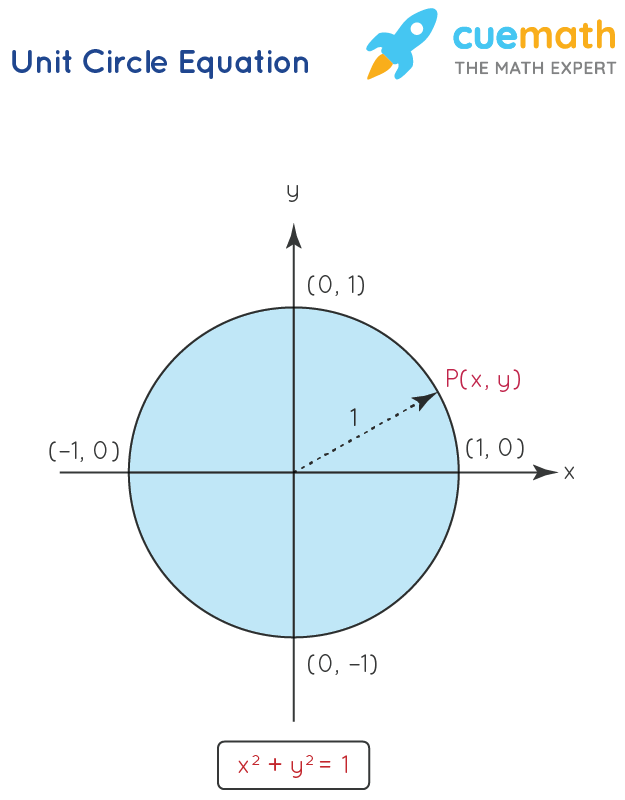
Equation of a Unit of measurement Circle
The full general equation of a circle is (x - a)2 + (y - b)2 = r2, which represents a circumvolve having the center (a, b) and the radius r. This equation of a circle is simplified to represent the equation of a unit circumvolve. A unit circumvolve is formed with its eye at the bespeak(0, 0), which is the origin of the coordinate axes. and a radius of 1 unit. Hence the equation of the unit circle is (10 - 0)ii + (y - 0)2 = 12. This is simplified to obtain the equation of a unit circle.
Equation of a Unit of measurement Circle: xtwo + y2 = 1
Here for the unit circle, the centre lies at (0,0) and the radius is one unit. The above equation satisfies all the points lying on the circumvolve across the four quadrants.
Finding Trigonometric Functions Using a Unit of measurement Circumvolve
Nosotros can summate the trigonometric functions of sine, cosine, and tangent using a unit circumvolve. Let us utilise the Pythagoras theorem in a unit circle to understand the trigonometric functions. Consider a right triangle placed in a unit of measurement circumvolve in the cartesian coordinate plane. The radius of the circle represents the hypotenuse of the right triangle. The radius vector makes an angle θ with the positive x-axis and the coordinates of the endpoint of the radius vector is (x, y). Here the values of x and y are the lengths of the base and the altitude of the right triangle. Now we accept a right angle triangle with the sides 1, x, y. Applying this in trigonometry, nosotros tin can observe the values of the trigonometric ratio, as follows:
- sinθ = Altitude/Hypoteuse = y/1
- cosθ = Base of operations/Hypotenuse = 10/1
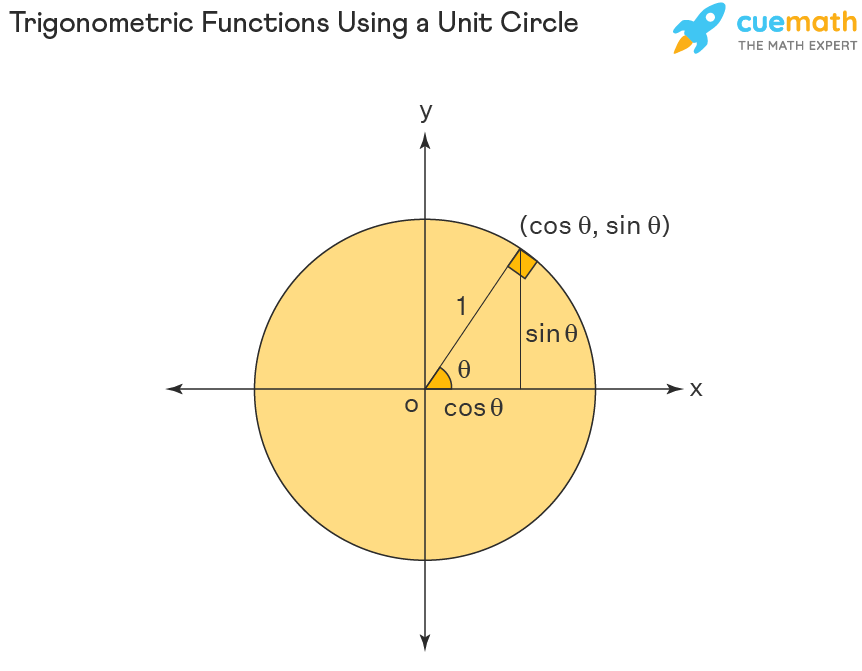
We now have sinθ = y, cosθ = x, and using this we now take tanθ = y/x. Similarly, we can obtain the values of the other trigonometric ratios using the right-angled triangle inside the unit circle. Also by changing the θ values we can obtain the primary values of these trigonometric ratios.
Unit of measurement Circle with Sin Cos and Tan
Whatsoever point on the unit of measurement circle has coordinates(x, y), which are equal to the trigonometric identities of (cosθ, sinθ). For any values of θ made by the radius line with the positive x-centrality, the coordinates of the endpoint of the radius represent the cosine and the sine of the θ values. Hither we have cosθ = x, and sinθ = y, and these values are helpful to compute the other trigonometric ratio values. Applying this further we have tanθ = sinθ/cosθ or tanθ = y/ten.
Another important point to be understood is that the sinθ and cosθ values e'er lie between 1 and -1, and the radius value is 1, and information technology has a value of -1 on the negative ten-axis. The entire circle represents a complete angle of 360º and the four quadrant lines of the circumvolve brand angles of 90º, 180º, 270º, 360º(0º). At 90º and at 270º the cosθ value is equal to 0 and hence the tan values at these angles are undefined.
Case: Find the value of tan 45º using sin and cos values from the unit circle.
Solution:
We know that, tan 45° = sin 45°/cos 45°
Using the unit circumvolve chart:
sin 45° = 1/√ii
cos 45° = 1/√2
Therefore, tan 45° = sin 45°/cos 45°
= (1/√ii)/(1/√2)
= i
Answer: Therefore, tan 45° = 1
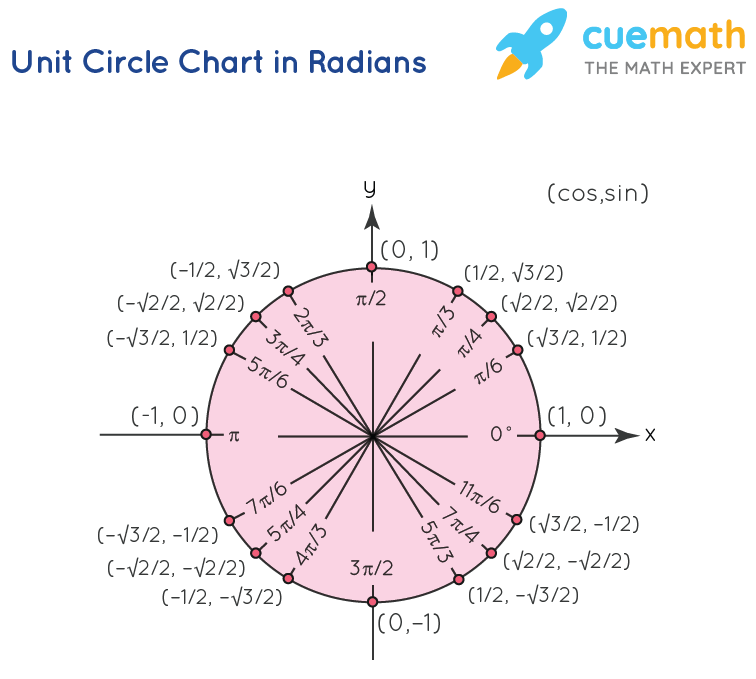
Unit of measurement Circle Chart in Radians
The unit circle represents a complete angle of 2π radians. And the unit circle is divided into four quadrants at angles of π/2, π. 3π/2, and 2π respectively. Further within the showtime quadrant at the angles of 0, π/6, π/4, π/iii, π/two are the standard values, which are applicable to the trigonometric ratios. The points on the unit circle for these angles represent the standard angle values of the cosine and sine ratios. On close ascertainment of the beneath figure the values are repeated across the four quadrants, but with a modify in sign. This change in sign is because of the reference 10-axis and y-centrality, which are positive on one side and negative on the other side of the origin. At present with the help of this, nosotros can easily find the trigonometric ratio values of standard angles, across the iv quadrants of the unit circumvolve.
Unit of measurement Circle and Trigonometric Identities
The unit circle identities of sine, cosecant, and tangent tin be further used to obtain the other trigonometric identities such as cotangent, secant, and cosecant. The unit of measurement circumvolve identities such as cosecant, secant, cotangent are the corresponding reciprocal of the sine, cosine, tangent. Further, we can obtain the value of tanθ by dividing sinθ with cosθ, and we can obtain the value of cotθ by dividing cosθ with sinθ.
For a right triangle placed in a unit circle in the cartesian coordinate plane, with hypotenuse, base of operations, and distance measuring 1, x, y units respectively, the unit circumvolve identities can be given as,
- sinθ = y/1
- cosθ = x/1
- tanθ = sinθ/cosθ = y/x
- sec(θ = 1/10
- csc(θ) = ane/y
- cot(θ) = cosθ/sinθ = x/y
Unit of measurement Circle Pythagorean Identities
The 3 of import Pythagorean identities of trigonometric ratios tin exist easily understood and proved with the unit circle. The Pythagoras theorem states that in a correct-angled triangle the square of the hypotenuse is equal to the sum of the square of the other two sides. The three Pythagorean identities in trigonometry are as follows.
- siniiθ + cos2θ = 1
- one + taniiθ = seciiθ
- 1 + cot2θ = cosec2θ
Here we shall try to show the offset identity with the assist of the Pythagoras theorem. Let u.s.a. take x and y as the legs of the correct-angled triangle having a hypotenuse 1 unit. Applying Pythagoras theorem nosotros have x2 + y2 = 1 which represents the equation of a unit of measurement circle. Also in a unit circle, nosotros have, x = cosθ, and y = sinθ, and applying this in the above statement of the Pythagoras theorem, nosotros take, cos2θ + sin2θ = i. Thus we have successfully proved the first identity using the Pythagoras theorem. Further inside the unit circle, we can also show the other two Pythagorean identities.
Unit of measurement Circle and Trigonometric Values
The diverse trigonometric identities and their principal angle values can be calculated through the use of a unit circle. In the unit circle, we have cosine as the x-coordinate and sine as the y-coordinate. Let usa now find their corresponding values for θ = 0°, and θ = 90º.

For θ = 0°, the x-coordinate is 1 and the y-coordinate is 0. Therefore, we have cos0º = 1, and sin0º = 0. Let u.s. expect at another angle of 90º. Here the value of cos90º = 1, and sin90º = one. Farther, let us use this unit circumvolve and observe the of import trigonometric function values of θ such every bit 30º, 45º, 60º. As well, we tin also measure these θ values in radians. We know that 360° = 2π radians. Nosotros tin now convert the angular measures to radian measures and express them in terms of the radians.
Unit Circumvolve Table:
The unit circle tabular array is used to list the coordinates of the points on the unit circumvolve that corresond to mutual angles with the help of trigonometric ratios.
| Angle θ | Radians | Sinθ | Cosθ | Tanθ = Sinθ/Cosθ | Coordinates |
|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 | (1, 0) |
| xxx° | π/6 | 1/2 | √iii/2 | 1/√3 | (√3/ii, 1/2) |
| 45° | π/four | 1/√2 | 1/√ii | 1 | (1/√2, 1/√2) |
| 60° | π/3 | √3/2 | 1/2 | √three | (1/2, √3/ii) |
| 90° | π/two | 1 | 0 | undefined | (0,1) |
We can find the secant, cosecant, and cotangent functions also using these formulas:
- secθ = ane/cosθ
- cosecθ = ane/sinθ
- cotθ = ane/tanθ
Nosotros accept discussed the unit circle for the outset quadrant. Similarly, we can extend and detect the radians for all the unit circle quadrants. The numbers ane/2, one/√ii, √three/2, 0, 1 echo forth with the sign in all 4 quadrants.
Unit Circle in Complex Airplane
A unit circle consists of all circuitous numbers of accented value as 1. Therefore, it has the equation of |z| = i. Any complex number z = x + \(i\)y volition lie on the unit circumvolve with equation given as tentwo + y2 = 1.
The unit circle tin be considered as unit complex numbers in a circuitous plane, i.east., the set of complex numbers z given by the grade,
z = east\(i\)t = cos t + \(i\) sin t = cis(t)
The relation given above represents Euler's formula.
Unit Circle Examples
become to slidego to slidego to slide
FAQs on Unit Circle
What is Unit of measurement Circle in Math?
A unit circle is a circle with a radius of one unit. Generally, a unit circle is represented in the coordinate aeroplane with its middle at the origin. The equation of the unit of measurement circumvolve of radius one unit of measurement and having the center at (0, 0) is x2 + y2 = 1. Farther, the unit circle has applications in trigonometry and is used to find the principal values of sine and cosine trigonometric ratios.
How Do yous Find Sin and Cos Using the Unit Circle?
The unit circumvolve can exist used to find the values of sinθ and Cosθ. In a unit circle of radius 1 unit and having the eye at (0, 0), allow united states take a radius inclined to the positive x-axis at an angle θ, and the endpoint of the radius equally (x, y). Describe a perpendicular from the end of the radius to the x-centrality and it forms a correct-angled triangle with the radius as the hypotenuse. The adjacent side of this triangle is the x value, the opposite side of the triangle is the y value and the hypotenuse is of i unit of measurement. Further using the trigonometric ratio formula we have sinθ = Opp/Hyp = y/i, and cosθ = Adj/Hyp = x/i. Thus we have sinθ = y, and cosθ = x.
What is the Unit of measurement Circle Definition of Trig Functions?
The trigonometric office can be calculated for the principal values using the unit circumvolve. For a unit circle having the center at the origin(0, 0), the radius of 1 unit, if the radius is inclined at an bending θ and the endpoint of the radius vector is (ten, y), then cosθ = x and sinθ = y. Further, all the other trigonometric ratios tin be calculated from these two values. As well, the chief values tin can exist computed by changing the θ value.
How to Find Terminal Betoken on Unit Circle?
The terminal point on a unit of measurement circle tin be found with the help of the equation of the unit of measurement circle tentwo + yii = 1. If the given point satisfies this equation then it is a signal lying on the unit circle. Further, the terminal point on the unit of measurement value can be found for the θ value, by finding the values of cosθ and sinθ.
What is the Equation of Unit of measurement Circle?
The equation of a unit circle is 102 + y2 = 1. Here it is considered that the unit circle has its center at the origin(0, 0) of the coordinate axes, and has a radius of one unit. This equation of unit circle has been derived using the help of the altitude formula.
How Do you Derive the Equation of a Unit Circumvolve?
The equation of a unit circle tin can be calculated using the distance formula of coordinate geometry. For a circle having the middle at the origin(0, 0), the radius of i unit of measurement, whatever betoken on the circle tin be taken as (10, y). Applying the definition of a circle, and using the altitude formula nosotros accept (x - 0)2 + (y - 0)2 = one, which can be simplified as xtwo + ytwo = i.
When is Tan Undefined on the Unit Circle?
The unit circle having an equation of ten2 + y2 = 1 is helpful to notice the trigonometric ratios of sinθ = y and cosθ = x. Using these values we can conveniently notice the value of tanθ = sinθ/cosθ = y/x. Tanθ will be undefined for cosθ = 0, i.due east., when θ is equal to ninety° and 270°.
What is the Connexion Between Right Triangles and the Unit Circle?
The correct triangles and a unit circle are uniquely connected. Any point on the unit circle can be visualized as a right triangle with radius as the hypotenuse of the right triangle and the coordinates of the betoken as the other 2 sides of the right triangle. The equation of a circumvolve 102 + y2 = one completely satisfies the Pythagoras theorem related to the correct triangle. Besides, the correct triangle within the unit circle is helpful to derive the trigonometric ratio values.
What is the Unit Circumvolve Used for?
The unit circle is prominently useful in trigonometry. For the trigonometric ratios of sinθ, cosθ, tanθ, their principal angle values of 0º, 30º, 45º, 60º, 90º can be easily calculated using the unit circle. Additionally, the unit circle is useful to represent complex numbers in the argand airplane.
What are the Quadrants of the Unit of measurement Circle?
The unit circle has four quadrants similar to the quadrants in the coordinate arrangement. The four quadrants are of equal area and they represent one-quaternary of the area of the circumvolve. Each of the quadrants subtends an angle of 90º or a right angle at the heart of the circle.
How Do yous Describe a Unit of measurement Circle in Terms of Complex Numbers?
A unit circumvolve consists of all complex numbers of absolute value as one, thus any complex number z = ten + \(i\)y will prevarication on the unit circle with equation given every bit xii + y2 = 1. Therefore, the equation of the unit circumvolve can exist given as |z| = ane.
Tangent Lines Of A Circle,
Source: https://www.cuemath.com/geometry/unit-circle/
Posted by: walkerdeboyfaing.blogspot.com


0 Response to "Tangent Lines Of A Circle"
Post a Comment